Day 4 - Topological Space
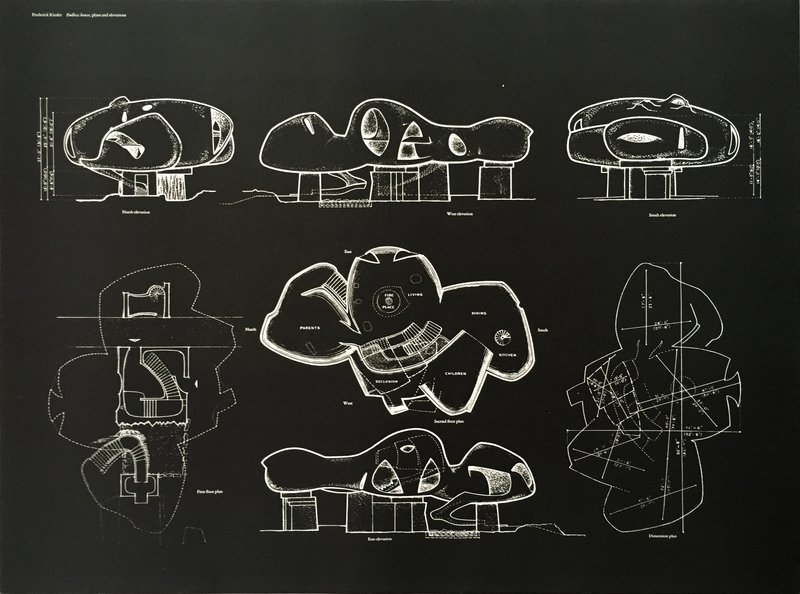
The explosive instantiation that emerges from the parametric definition of space typically exhausts its limits for differentiation at the space of topology. As a highly abstract form of geometry, topological and organizational space are founded in Euler's solution to the 'urban' problem of the Seven Bridges of Königsberg. Euler also famously discovered the formula V-E+F=2, which describes the relationship between the vertices, edges and faces of any polyhedron. A rigorous understanding of topological operations becomes critical for architectural design. Older typological hierarchies are challenged by the rigorous definition of topological manifolds. In this class we study the Endless House by Frederick Kiesler; a radical work that redefines architecture through abstract concepts of 'connectivity', 'corealation' an'biotechnique'. We explore the limitation of NURBS as a topological tool and expand an essential toolkit for modelling with subdivision surfaces and meshes. In the representation tutorial we look at procedural texture mapping as well as slit-scan photography.
![]()
The explosive instantiation that emerges from the parametric definition of space typically exhausts its limits for differentiation at the space of topology. As a highly abstract form of geometry, topological and organizational space are founded in Euler's solution to the 'urban' problem of the Seven Bridges of Königsberg. Euler also famously discovered the formula V-E+F=2, which describes the relationship between the vertices, edges and faces of any polyhedron. A rigorous understanding of topological operations becomes critical for architectural design. Older typological hierarchies are challenged by the rigorous definition of topological manifolds. In this class we study the Endless House by Frederick Kiesler; a radical work that redefines architecture through abstract concepts of 'connectivity', 'corealation' an'biotechnique'. We explore the limitation of NURBS as a topological tool and expand an essential toolkit for modelling with subdivision surfaces and meshes. In the representation tutorial we look at procedural texture mapping as well as slit-scan photography.